Spearman’s Rangkorrelationskoeffizienten bestimmen und interpretieren

Den Rangkorrelationskoeffizient nach Spearman wird verwendet, um den Zusammenhang zwischen zwei mindestens ordinalskalierten Variablen zu bestimmen.

Anhand des Rangkorrelationskoeffizienten können wir Aussagen darüber treffen, ob zwei Variablen zusammenhängen, und wenn ja, wie stark der Zusammenhang ist und in welche Richtung er besteht.

Der Rangkorrelationskoeffizient nach Spearman wird auch als Spearman‘s Rho () bezeichnet.

Scribbrs kostenlose Rechtschreibprüfung

Fehler kostenlos beheben

Spearman‘s ρ am Beispiel erklärt

Nehmen wir an, wir haben acht Studierende nach ihren Abiturnoten in den Fächern Deutsch und Englisch gefragt und folgende Antworten erhalten.

Nun möchten wir den Zusammenhang zwischen den beiden Variablen bestimmen und berechnen dazu den Rangkorrelationskoeffizienten.

Als Ergebnis erhalten wir = 0.19. Daraus können wir ablesen, dass es einen positiven Zusammenhang zwischen den Punktzahlen in den Fächern Deutsch und Englisch gibt, dieser allerdings nicht sehr stark ist.

Den Rangkorrelationskoeffizienten in 5 Schritten bestimmen

In der folgenden Tabelle schauen wir uns die einzelnen Berechnungsschritte genauer an.

	Allgemein	Beispiel
1	Bestimme zunächst für jeden Fall den Rang für beide Variablen einzeln.	Wir vergeben jeweils die Ränge 1–8 für die Punkte in den Fächern Deutsch und Englisch. Person Punkte in Deutsch Rang Punkte in Englisch Rang 1 14 2 11 5 2 8 6 15 1 3 11 4 8 8 4 6 8 10 6 5 15 1 13 3 6 13 3 12 4 7 7 7 9 7 8 9 5 14 2
2	Bestimme die Differenz der Ränge der beiden Variablen und quadriere das Ergebnis.	Wir berechnen für jeden Fall einzeln die Differenz zwischen den Rängen der Noten. Person 1 2 – 5 = -3 (-3)2 = 9 2 6 – 1 = 5 52 = 25 3 4 – 8 = -4 (-4)2 = 16 4 8 – 6 = 2 22 = 4 5 1 – 3 = -2 (-2)2 = 4 6 3 – 4 = -1 (-1)2 = 1 7 7 – 7 = 0 02 = 0 8 5 – 2 = 3 32 = 9
3	Bilde die Summe aus den quadrierten Differenzen und multipliziere das Ergebnis mit 6.	Wir addieren die Ergebnisse von Schritt 2 und multiplizieren die Summe mit 6. 9 + 25 + 16 + 4 + 4 + 1 + 0 + 9 = 68 68 * 6 = 408
4	Berechne:	Wir setzen die Gesamtanzahl der untersuchten Fälle (n = 8) in  ein.
5	Setze alle berechneten Werte in die Formel ein:	Wir setzen alle Ergebnisse aus den Schritten 1-4  in die Formel ein:

Möchtest du eine fehlerfreie Arbeit abgeben?

Mit einem Lektorat helfen wir dir, deine Abschlussarbeit zu perfektionieren.

Neugierig? Bewege den Regler von links nach rechts!

Zu deiner Korrektur

Formel zum Rangkorrelationskoeffizienten ρ

Die Formel fasst die oben erläuterten Schritte zusammen.

Formel zum Rangkorrelationskoeffizienten nach Spearman
oder rsp	Rangkorrelationskoeffizient
	Rang für Fall i in der geordneten Datenreihe für Variable 1
	Rang für Fall i in der geordneten Datenreihe für Variable 2
	Gesamtanzahl der Fälle

Den Rangkorrelationskoeffizienten richtig interpretieren

Der Rangkorrelationskoeffizient liegt immer zwischen -1 und 1.

Dabei zeigt uns der Wert, ob ein Zusammenhang besteht, und wenn ja, wie stark dieser ist und in welche Richtung er besteht.

Richtung des Zusammenhangs

Ein positiver Korrelationskoeffizient zeigt auf, dass ein positiver Zusammenhang zwischen den zwei Variablen besteht. Das bedeutet, dass, wenn der Wert der einen Variablen steigt, dies auch für die andere Variable der Fall ist.

Bei einem negativen Koeffizienten verlaufen die Variablen gegenläufig. Wenn also der Wert der einen Variablen steigt, sinkt der Wert der anderen Variablen.

Stärke des Zusammenhangs

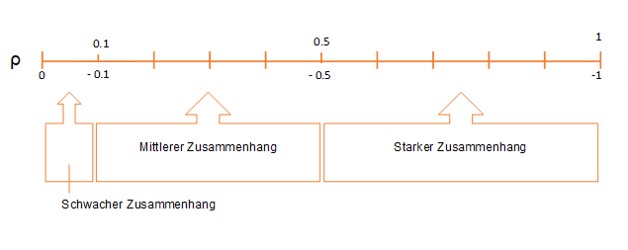
Um eine Aussage über die Stärke des Zusammenhangs zu treffen, können wir die Einteilung nach Cohen verwenden. Dabei ist es allerdings wichtig zu beachten, dass es sich dabei um eine allgemeine Einteilung handelt und der Rangkorrelationskoeffizient stets in Bezug zum Kontext interpretiert werden sollte, in dem er erhoben und bestimmt wurde.

Die Grafik gibt dir einen Überblick über die Stärke des Zusammenhangs für deinen -Wert.

r = 0 → kein linearer Zusammenhang
r = 1 oder -1 → vollständiger linearer Zusammenhang

Voraussetzungen Rangkorrelationskoeffizient

Um den Rangkorrelationskoeffizienten bestimmen zu können, müssen die Daten mindestens ordinalskaliert sein. Weitere Annahmen, wie beispielsweise eine Normalverteilung der Daten wie beim Korrelationskoeffizienten nach Pearson, müssen nicht erfüllt sein.

Möchtest du eine fehlerfreie Arbeit abgeben?

Mit einem Lektorat helfen wir dir, deine Abschlussarbeit zu perfektionieren.

Neugierig? Bewege den Regler von links nach rechts!

Zu deiner Korrektur

Häufig gestellte Fragen

Was sagt der Rangkorrelationskoeffizient aus?

Der Rangkorrelationskoeffizient nach Spearman gibt uns Auskunft über den Zusammenhang zwischen zwei mindestens ordinalskalierten Variablen.

Anhand des Rangkorrelationskoeffizienten können wir sagen, ob zwei Variablen zusammenhängen, und wenn ja, wie stark der Zusammenhang ist und in welche Richtung er besteht.

Was ist Spearman’s Rho (ρ)?

Spearman’s Rho ist lediglich eine andere Bezeichnung für den Rangkorrelationskoeffizienten nach Spearman.

Was ist der Unterschied zwischen der Pearson- und der Spearman-Korrelation?

Wann wir welchen Korrelationskoeffizienten verwenden, hängt vom Skalenniveau unserer Daten ab. Um die Korrelation nach Pearson zu berechnen, benötigen wir metrische Daten. Spearman’s Rangkorrelationskkoeffizienten verwenden wir für ordinalskalierte Daten.