Normalverteilung verstehen und interpretieren - mit Beispiel
Die Normalverteilung wird verwendet, um Häufigkeiten von Daten und Beobachtungen darzustellen.
Andere Bezeichnungen für die Normalverteilung sind Gauß-Verteilung (nach dem deutschen Mathematiker Carl Friedrich Gauß) und aufgrund des Verlaufs des Graphen auch Glockenkurve.
In der Abbildung kannst du am glockenförmigen Verlauf der roten Linie direkt sehen, woher dieser Name stammt.
Beispiel zur Normalverteilung
Eine Normalverteilung liegt immer dann vor, wenn wir eine große Stichprobe, also viele Beobachtungsdaten haben, wie zum Beispiel bei der Verteilung der Körpergröße in einer Stadt.
Nehmen wir an, wir haben zufällig 5000 Bewohner einer Stadt ausgewählt und ihre Körpergröße gemessen.
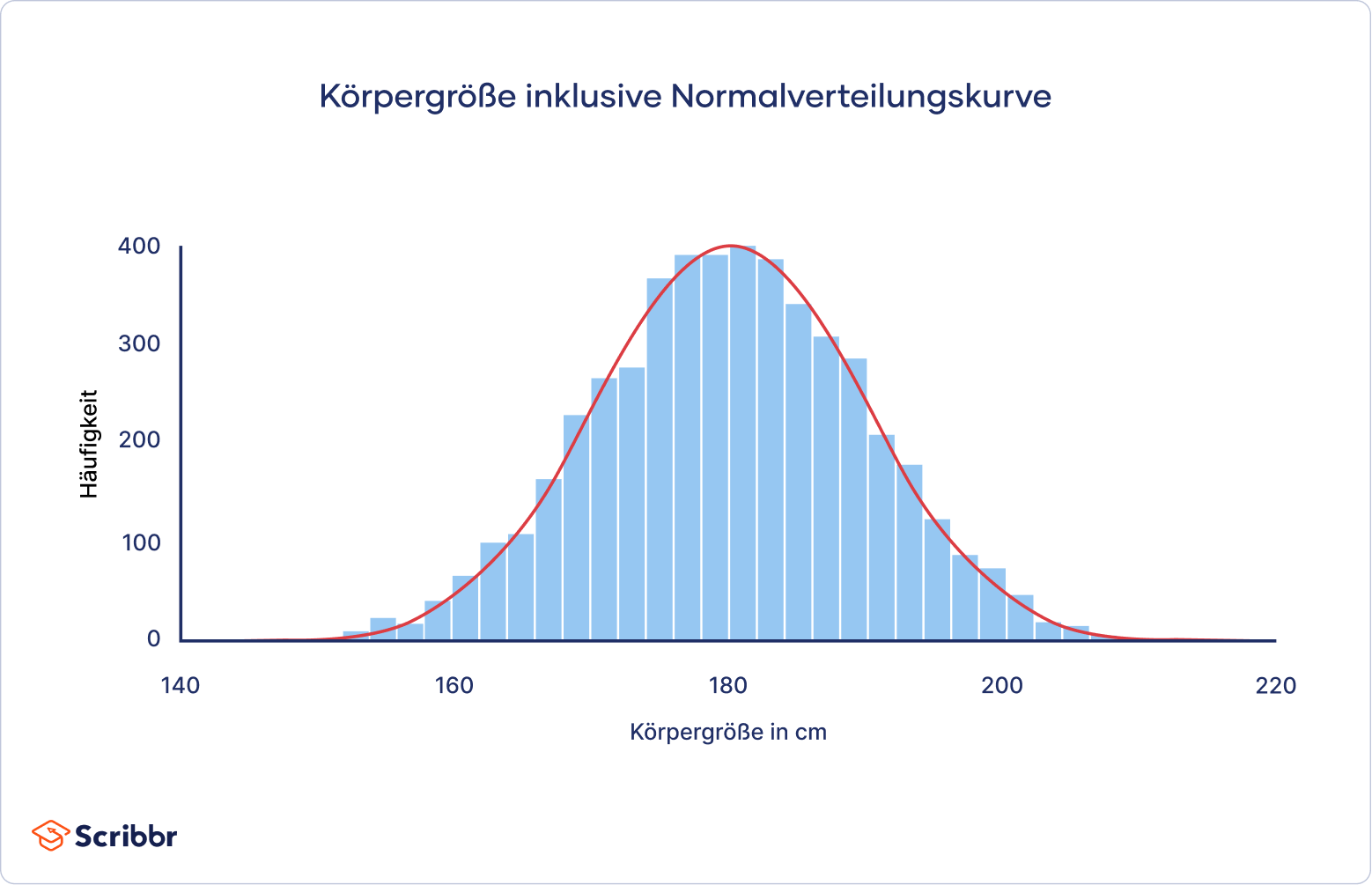
Das Säulendiagramm zeigt die Verteilung der Körpergrößen. Auf der horizontalen Achse (x-Achse) sehen wir die Körpergrößen der Bewohner und auf der senkrechten Achse (y-Achse), wie häufig diese in der Stichprobe vorkommen.
Wir können bereits an dem Diagramm ablesen, dass die meisten Menschen in der Stadt etwa 1.80 m groß sind.
Je kleiner die Säulen sind, desto seltener kommt die dazugehörige Körpergröße vor. So sehen wir auch auf den ersten Blick, dass sehr wenige Bewohner kleiner als 1.60 m oder größer als 2.00 m sind.
Außerdem sind die Daten symmetrisch um den Mittelwert verteilt, d. h. eine Hälfte der Bewohner ist kleiner als 1.80 m und die andere größer.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Der Graph der Normalverteilung
Der Graph der Funktion der Normalverteilung ist die rote Linie in der Abbildung oben und zeigt die Verteilung der Daten um den Mittelwert, in unserem Beispiel also um die mittlere Körpergröße von 1.80 m.
Um den Graphen der Normalverteilung zu verstehen, sind zwei Parameter relevant:
- der Erwartungswert (μ), dies ist auch der Mittelwert
- die Standardabweichung um den Mittelwert (σ)
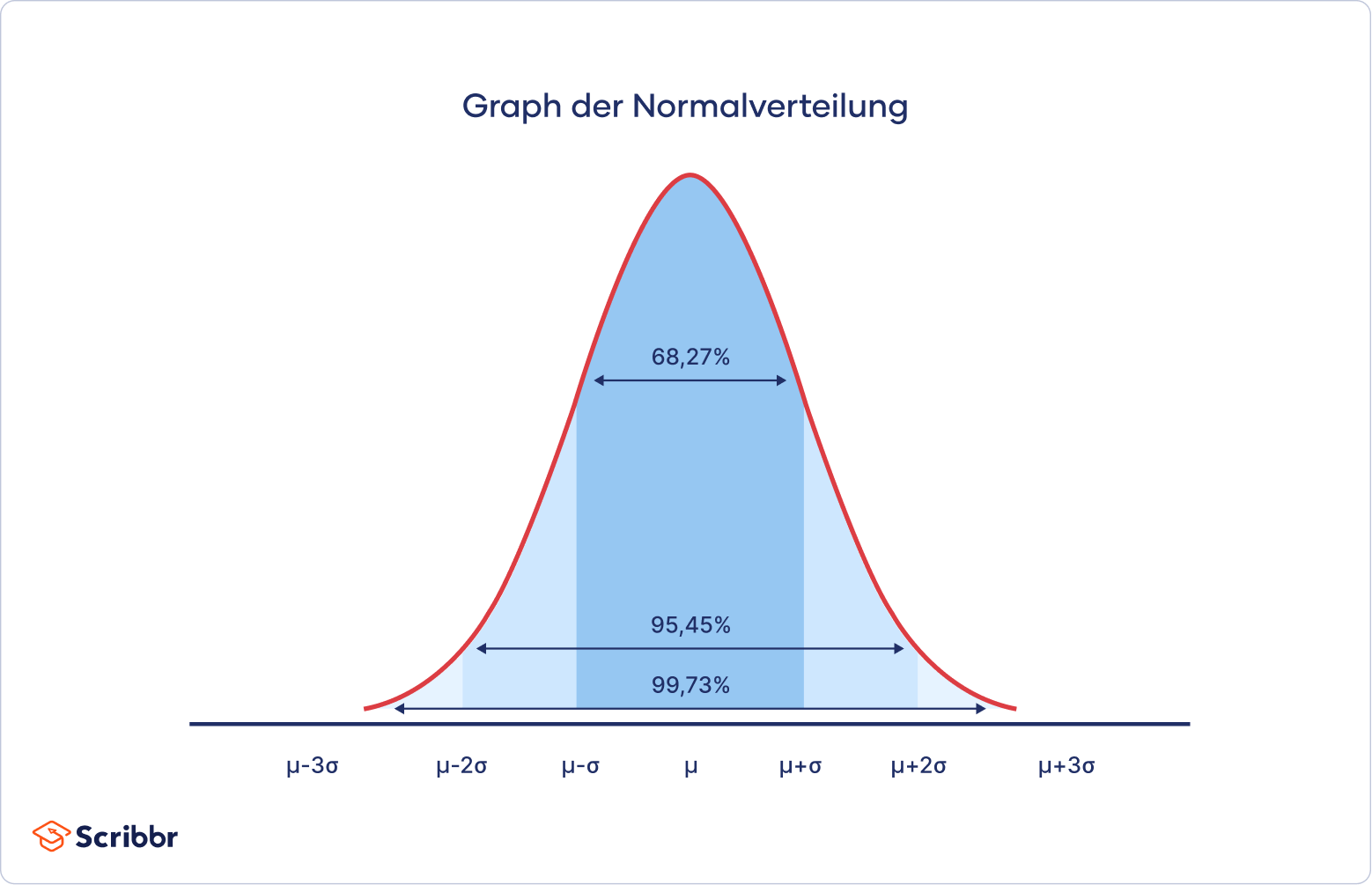
Der Graph der Normalverteilung zeigt, dass …
- 68,27 % aller Werte im Intervall von einer Standardabweichung,
- 95,45 % aller Werte im Intervall von zwei Standardabweichungen,
- 99,73 % aller Werte im Intervall von drei Standardabweichungen
… um den Erwartungswert liegen.
Interpretationen der Normalverteilung am Beispiel erklärt
| Wert | Interpretation | Beispiel |
|---|---|---|
| μ | Mittelwert (Erwartungswert) | Die durchschnittliche Körpergröße in der Stadt beträgt 1.80 m. |
| σ | Standardabweichung | Die Standardabweichung der Körpergröße in der Stadt beträgt 10 cm. |
| μ – σ | 34.1 % der Werte liegen innerhalb einer Standardabweichung unterhalb des Erwartungswerts | Die Körpergröße von 34.1 % der Bewohner liegt zwischen 1.70 m und 1.80 m. |
| μ + σ | 34.1 % der Werte liegen innerhalb einer Standardabweichung oberhalb des Erwartungswerts | Die Körpergröße von 34.1 % der Bewohner liegt zwischen 1.80 m und 1.90 m. |
| μ – 2σ | 47.7 % der Werte liegen innerhalb von zwei Standardabweichungen unterhalb des Erwartungswerts | Die Körpergröße von 47.7 % der Bewohner liegt zwischen 1.60 m und 1.80 m. |
| μ +2σ | 47.7 % der Werte liegen innerhalb von zwei Standardabweichungen oberhalb des Erwartungswerts | Die Körpergröße von 47.7 % der Bewohner liegt zwischen 1.80 m und 2.00 m. |
| μ – 3σ | 49.85 % der Werte liegen innerhalb von drei Standardabweichungen unterhalb des Erwartungswerts. | Die Körpergröße von 49.85 % der Bewohner liegt zwischen 1.50 m und 1.80 m. |
| μ + 3σ | 49.85 % der Werte liegen innerhalb von drei Standardabweichungen oberhalb des Erwartungswerts. | Die Körpergröße von 49.85 % der Bewohner liegt zwischen 1.80 m und 2.10 m. |
Verlauf des Graphen
Der Verlauf des Graphen der Normalverteilung kann unterschiedlich aussehen, je nachdem, welche Werte für den Mittelwert μ und die Standardabweichung σ vorliegen.
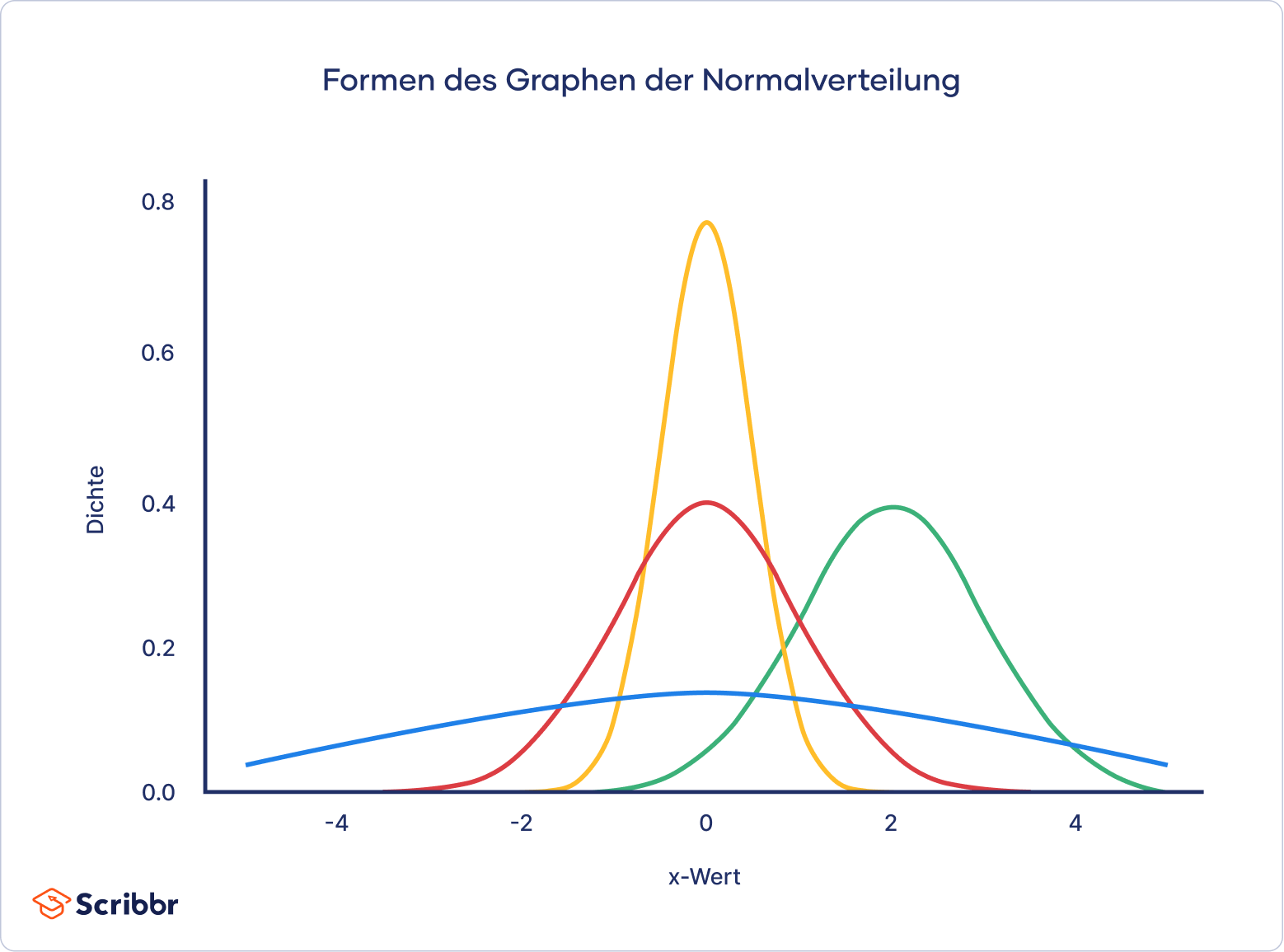
In der Abbildung siehst du verschiedene Beispielgraphen.
Der rote Graph ist der Graph der Standardnormalverteilung. Diese liegt vor, wenn wir einen Mittelwert von μ = 0 und eine Standardabweichung von σ = 1 haben.
| Graph in Abbildung | Vergleich zur Standardnormalverteilung |
|---|---|
| Rot (μ = 0, σ = 1) | Standardnormalverteilung |
| Gelb (μ = 0, σ = 0.5) | gestreckt, da σ < 1 ist. |
| Blau (μ = 0, σ = 3) | gestaucht, da σ > 1 ist. |
| Grün (μ = 2, σ = 1) | um 2 Einheiten nach rechts verschoben, da μ > 0. |
Der Mittelwert (μ) kennzeichnet, bei welchem x-Wert der höchste Punkt des Graphen liegt.
Ist der Mittelwert größer als 0, verschiebt sich der Graph nach rechts vom roten Graphen der Standardnormalverteilung. Bei einem Mittelwert kleiner als 0 verschiebt sich der Graph nach links.
Die Standardabweichung (σ) bestimmt, ob der Graph gestaucht oder gestreckt ist. Eine Stauchung bedeutet, dass der rote Graph breiter aussieht als der Graph der Standardnormalverteilung.
Eine Streckung bedeutet, dass der Graph schmaler aussieht im Vergleich zum roten Graphen der Standardnormalverteilung.
Funktion und Parameter der Normalverteilung
Die Funktion der Normalverteilung kannst du zum Beispiel verwenden, um den Graphen deiner Verteilung zu bestimmen.
Dazu kannst du einfach deine Werte für den Mittelwert μ und die Standardabweichung σ in die Formel einsetzen.
| Die Funktion der Normalverteilung | |
|---|---|
 |
|
 |
Zufallsvariable |
| μ |
|
 |
|
, die 
Häufig gestellte Fragen
- Was ist der Unterschied zwischen Normalverteilung und Gauß-Verteilung?
-
Es gibt keinen: Gauß-Verteilung ist lediglich eine andere Bezeichnung für die Normalverteilung. Das Gleiche gilt auch für die Bezeichnung Glockenkurve.
- Wofür wird die Normalverteilung verwendet?
-
Die Normalverteilung wird verwendet, um Häufigkeiten von Daten und Beobachtungen darzustellen.
Der Graph der Normalverteilung zeigt die Verteilung der Daten um den Mittelwert.
- Sieht der Graph der Normalverteilung immer gleich aus?
-
Nein, der Verlauf des Graphen der Normalverteilung hängt von den Werten für den Mittelwert μ und die Standardabweichung σ ab. Der Graph kann gestreckt oder gestaucht sowie nach rechts oder links verschoben sein.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2023, 09. Oktober). Normalverteilung verstehen und interpretieren - mit Beispiel. Scribbr. Abgerufen am 11. November 2024, von https://www.scribbr.de/statistik/normalverteilung/
