Korrelationskoeffizient nach Pearson berechnen und interpretieren

Der Korrelationskoeffizient nach Pearson, auch Korrelationskoeffizient nach Bravais-Pearson genannt, gibt uns Auskunft über den Zusammenhang von zwei metrisch skalierten Variablen.

Da es sich um einen standardisierten Koeffizienten handelt, können wir Zusammenhänge anhand des Korrelationskoeffizienten miteinander vergleichen.

Scribbrs kostenlose Rechtschreibprüfung

Fehler kostenlos beheben

Den Korrelationskoeffizienten nach Pearson berechnen

Zur Berechnung des Korrelationskoeffizienten kannst du z. B. SPSS, Excel oder Google Tabellen verwenden.

Den Korrelationskoeffizienten mit Excel oder Google Tabellen berechnen

Wir stellen dir unsere Excel-Datei und Google-Tabellen-Datei zur Verfügung, damit du die Berechnung damit üben kannst.

Geh in eine leere Zelle und gib die Formel = KORREL () für Excel oder = CORREL () für Google Tabellen ein.

Wähle die Daten aus beiden Spalten aus und trenne sie mit einem Semikolon.

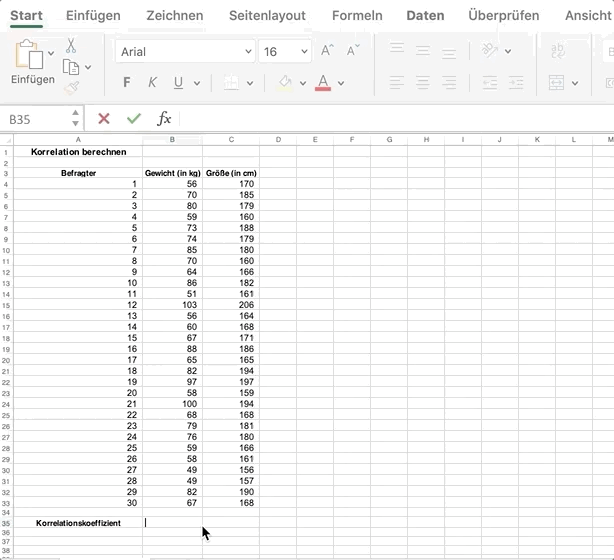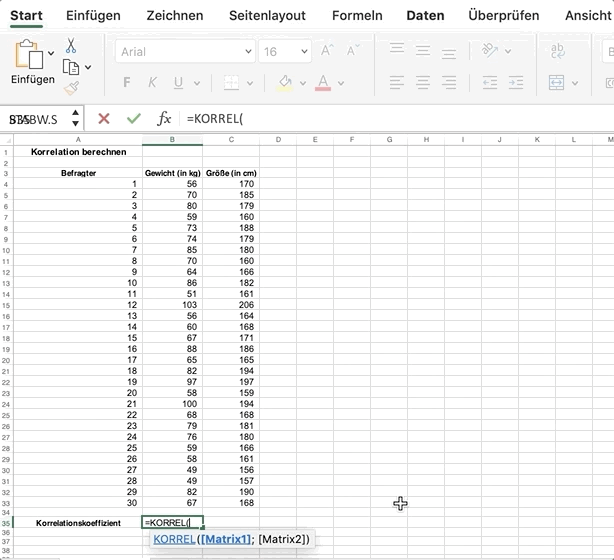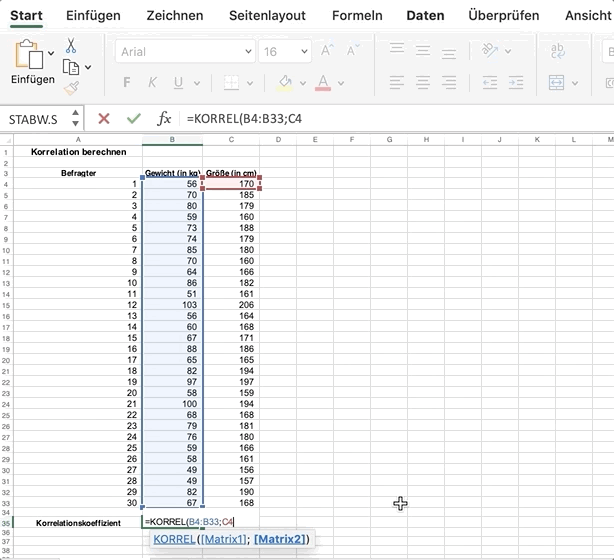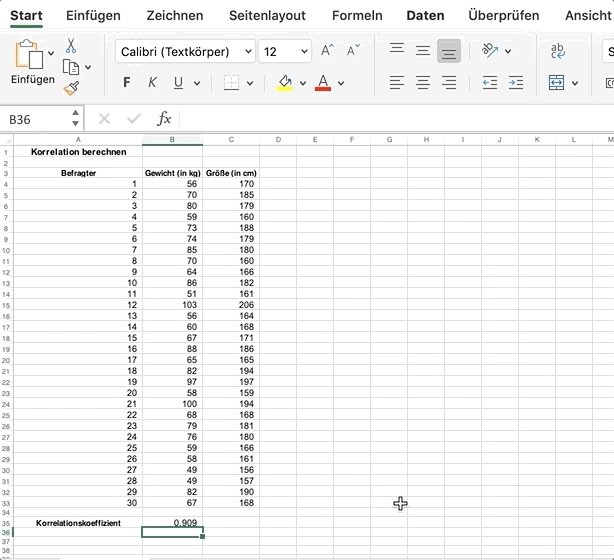
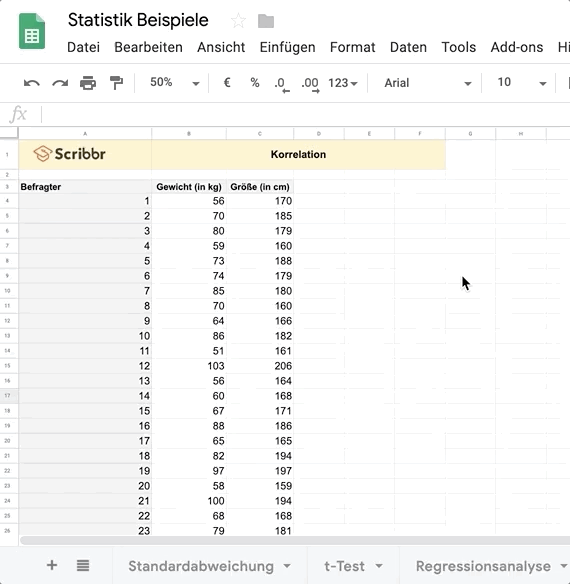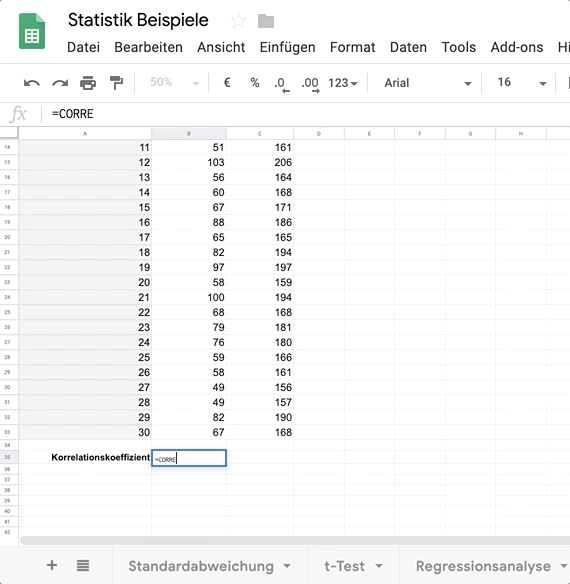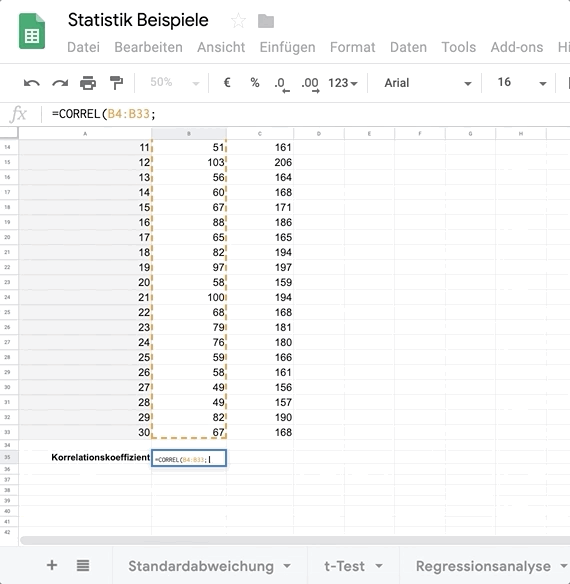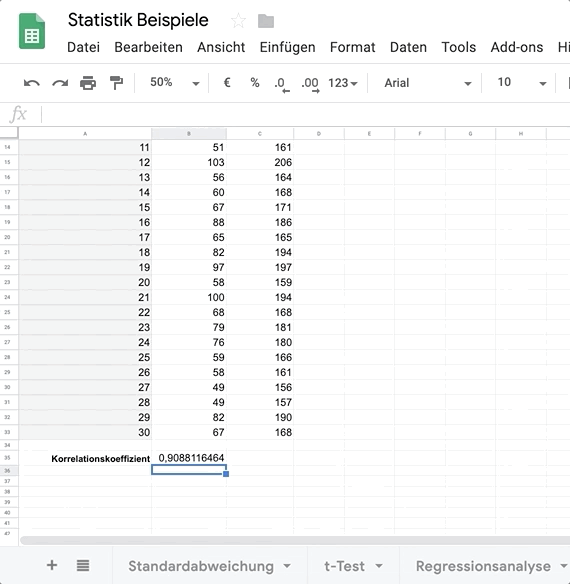
Du erhältst den Korrelationskoeffizienten der zwei Variablen, in diesem Fall Gewicht und Größe. Der Wert des Korrelationskoeffizienten muss dabei immer zwischen r = -1 und 1 liegen.

Den Korrelationskoeffizienten mit SPSS berechnen

Lade unsere SPSS-Datei herunter, damit du mit denselben Daten üben kannst.

Um den Korrelationskoeffizienten mit SPSS zu berechnen, klicke im Menü auf:

1. Analysieren
2. Korrelation
3. Bivariat

In dem neuen Fenster wählst du die Variablen aus, die du analysieren möchtest (Gewicht und Größe).

Kontrolliere, ob Pearson bei Korrelationskoeffizienten markiert ist, da du die lineare Korrelation ansehen möchtest.

Klicke auf Ok, um die Analyse durchzuführen. Du erhältst den Korrelationskoeffizienten, der immer zwischen -1 und 1 liegen muss.

Den Korrelationskoeffizienten in SPSS richtig interpretieren

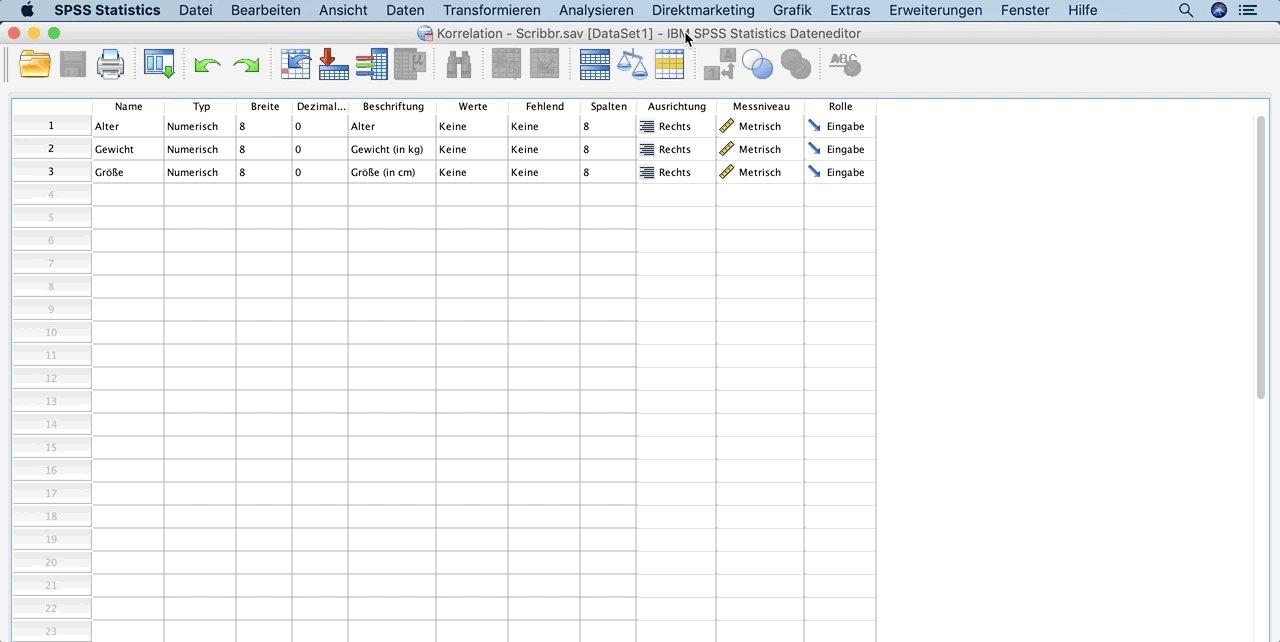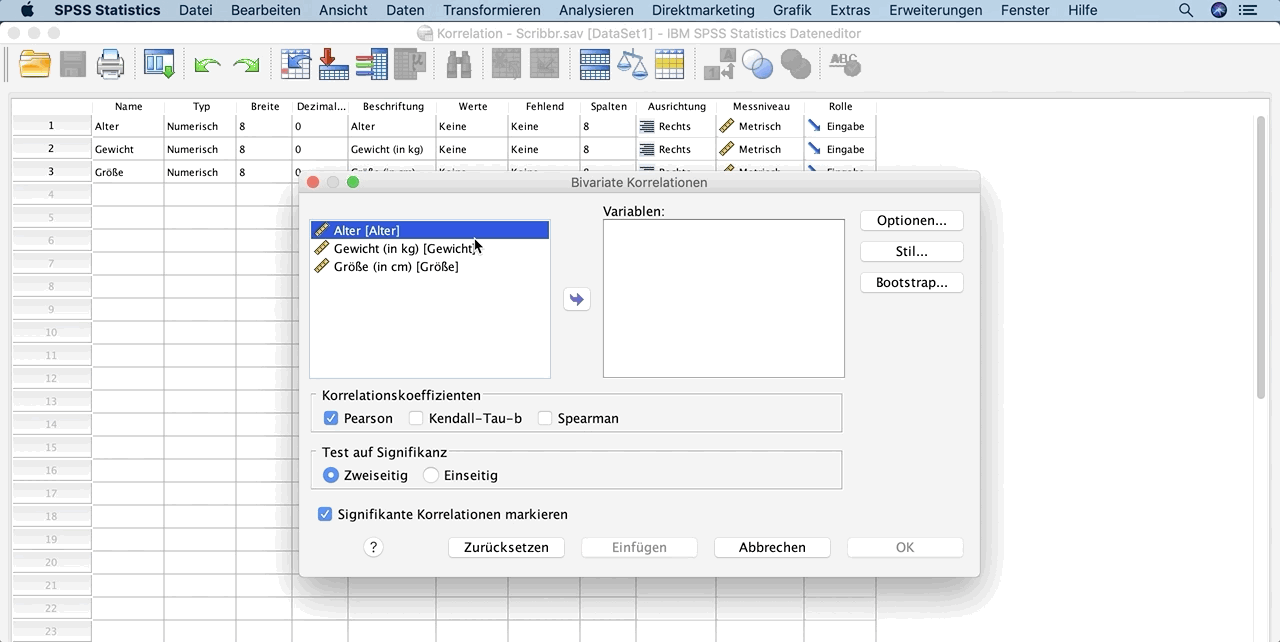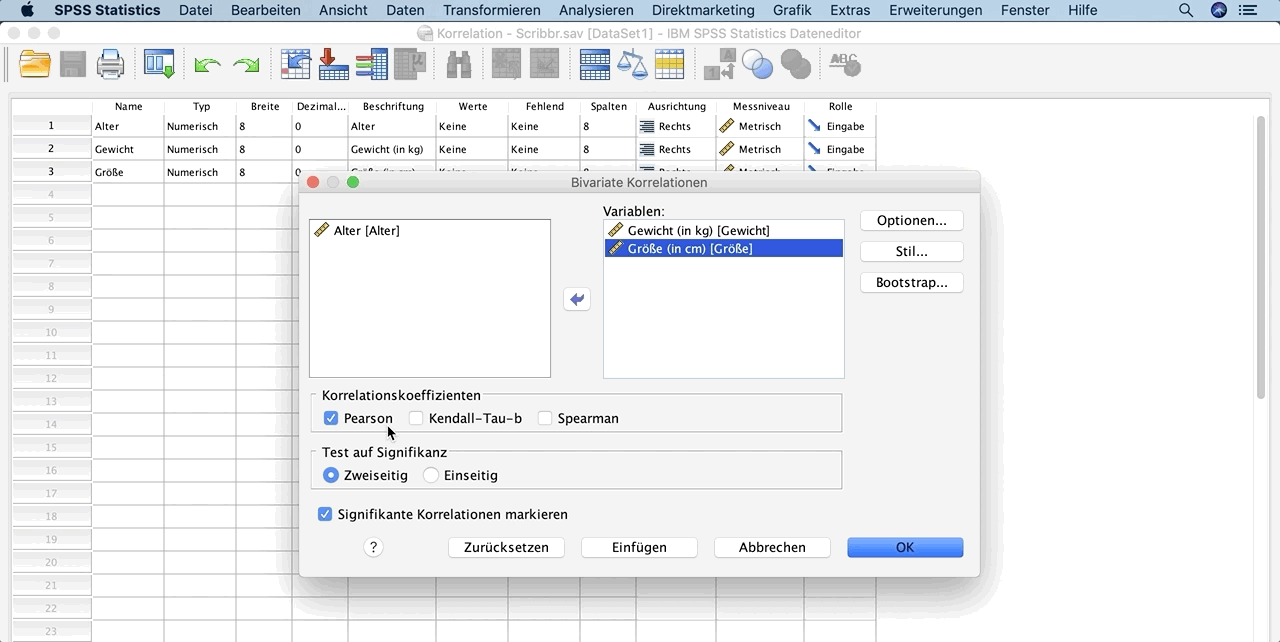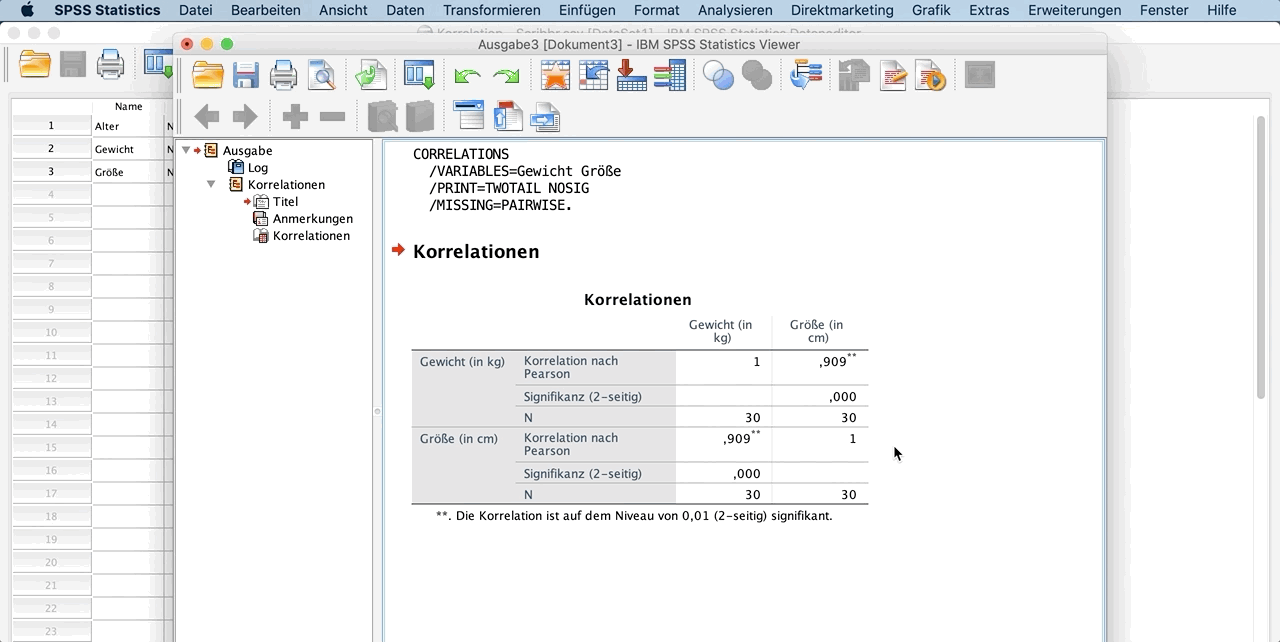
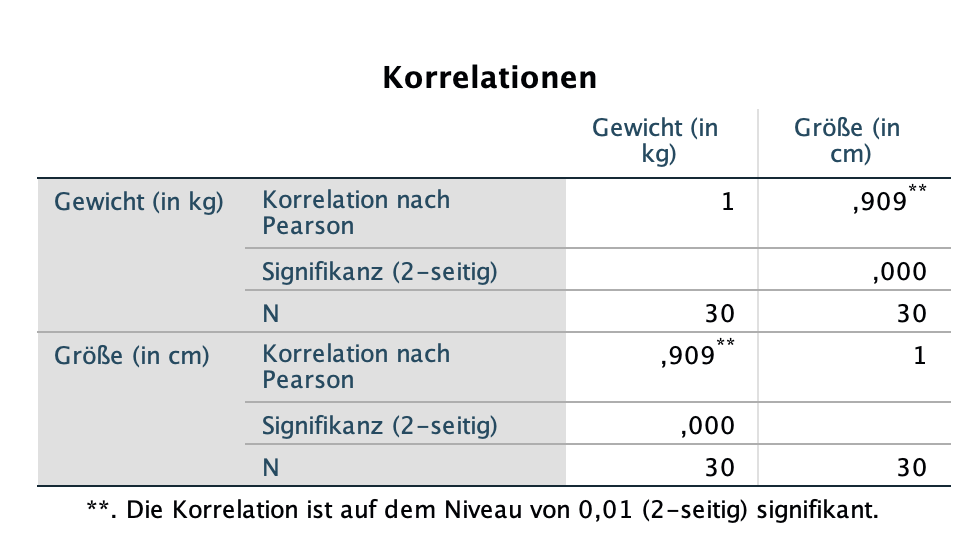
Berechnest du den Korrelationskoeffizienten mit SPSS, erhältst du bei unserem Beispiel die folgende Tabelle:

Möchtest du eine fehlerfreie Arbeit abgeben?

Mit einem Lektorat helfen wir dir, deine Abschlussarbeit zu perfektionieren.

Neugierig? Bewege den Regler von links nach rechts!

Zu deiner Korrektur

Formel zu Pearson‘s r

Um die Korrelation selbst zu berechnen, kannst du folgende Formel verwenden.

Formel zum Korrelationskoeffizient nach Pearson
r	Korrelationskoeffizient
xi	Beobachtungswerte der Variable x
yi	Beobachtungswerte der Variable y
	Arithmetisches Mittel aller Wert von x
	Arithmetisches Mittel aller Wert von y
N	Gesamtanzahl
sxy	Kovarianz der Variablen x und y
sx	Standardabweichung der Variable x
sy	Standardabweichung der Variable y

Pearson‘s r richtig interpretieren

Der Korrelationskoeffizient nach Pearson kann Werte zwischen -1 und 1 annehmen.

Dabei enthält der r-Wert Informationen über a) die Richtung und b) die Stärke des Zusammenhangs.

Richtung des Zusammenhangs

Ein positiver Korrelationskoeffizient zeigt auf, dass ein positiver Zusammenhang zwischen den zwei Variablen besteht. Das bedeutet, dass, wenn der Wert der einen Variablen steigt, dies auch für die andere Variable der Fall ist.

Bei einem negativen Korrelationskoeffizienten verlaufen die Variablen gegenläufig. Wenn also der Wert der einen Variablen steigt, sinkt der Wert der anderen Variablen.

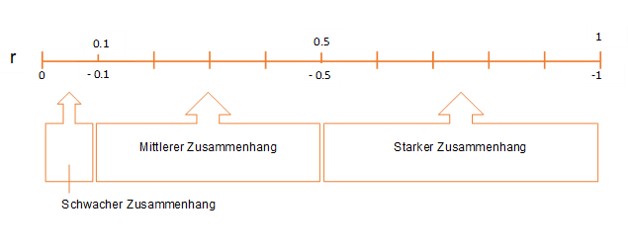
Stärke des Zusammenhangs

Um eine Aussage über die Stärke des Zusammenhangs zu treffen, können wir die Einteilung nach Cohen verwenden.

Dabei ist allerdings zu beachten, dass es sich um eine allgemeine Einteilung handelt und der Korrelationskoeffizient stets in Bezug zum Kontext interpretiert werden sollte, in dem er erhoben und bestimmt wurde.

Das Diagramm gibt dir einen Überblick über die Stärke des Zusammenhangs für deinen r-Wert.

r = 0 → kein linearer Zusammenhang
r = 1 oder -1 → vollständiger linearer Zusammenhang

Voraussetzungen für den Korrelationskoeffizient nach Pearson

Den Korrelationskoeffizienten nach Pearson kannst du anwenden, wenn die folgenden Annahmen erfüllt sind:

• Metrisches Skalenniveau
• Normalverteilung der Daten
• Linearer Zusammenhang zwischen den Variablen

Ergebnisse der Korrelation in der Abschlussarbeit zusammenfassen

Du beschreibst den Korrelationskoeffizienten im Ergebniskapitel deiner Bachelorarbeit oder Masterarbeit.

Häufig gestellte Fragen

Was sagt der Korrelationskoeffizient nach Pearson aus?

Der Korrelationskoeffizient nach Pearson gibt uns Auskunft über den Zusammenhang von zwei metrisch skalierten Variablen.

Ab wann ist meine Korrelation hoch?

Von einer hohen Korrelation wird bei einem r-Wert (Korrelationskoeffizient) zwischen 0.5 und 1 oder -0.5 und -1 gesprochen.

Wie kann ich den Korrelationskoeffizienten nach Pearson in Excel berechnen?

In Excel können wir den Korrelationskoeffizienten mit dem Befehl =KORREL() bestimmen. Gib dazu in den Klammern die Zellen an, für die du die Korrelation bestimmen möchtest. Trenne die Werte für die beiden Variablen mit einem Semikolon.

=KORREL(B2:B30;C2:C30)

Was ist der Unterschied zwischen der Pearson- und der Spearman-Korrelation?

Wann wir welchen Korrelationskoeffizienten verwenden, hängt vom Skalenniveau der Daten ab. Um die Korrelation nach Pearson zu berechnen, benötigen wir metrische Daten. Spearman‘s Rangkorrelationskoeffizienten verwenden wir für ordinalskalierte Daten.