Kostenlose Rechtschreibprüfung

Fehler kostenlos beheben

Kostenlose Plagiatsprüfung

Plagiate kostenlos finden

Korrektur deiner Abschlussarbeit

Fehler professionell beheben
  1. Home
  2. Wissensdatenbank
  3. Statistik
  4. Chi-Quadrat verstehen und berechnen

Chi-Quadrat verstehen und berechnen - mit Beispiel

Veröffentlicht am 12. Juni 2020 von Valerie Benning. Aktualisiert am 11. April 2023.

Chi-Quadrat χ2 gibt dir Auskunft über den Zusammenhang von zwei nominal– oder ordinalskalierten Variablen.

Beachte
Da es sich beim Chi-Quadrat-Koeffizienten um ein nicht-standardisiertes Zusammenhangsmaß handelt, ist nur eine begrenzte Interpretation möglich.

Scribbrs kostenlose Rechtschreibprüfung
rechtschreibpruefung-allgemein

Fehler kostenlos beheben

Chi-Quadrat am Beispiel erklärt

Nehmen wir an, wir wollen den Zusammenhang zwischen der Wahl der Studienrichtung und dem Geschlecht der Studierenden testen.

Dazu befragen wir insgesamt 250 Personen von drei verschiedenen Studienrichtungen, nämlich Jura, Naturwissenschaften (NW) und Sozialwissenschaften (SW), und erhalten folgende Antworten:

Jura NW SW Summe (Zeile)
Weiblich 38 35 57 130
Männlich 32 45 43 120
Summe (Spalte) 70 80 100 250

Nun möchten wir den Zusammenhang zwischen den beiden Variablen bestimmen und berechnen dazu den Chi-Quadrat-Koeffizienten.

Als Ergebnis erhalten wir einen Chi-Quadrat Wert von X^2=3.69.

Hier gilt es nun wieder, zu beachten, dass der Wert nicht standardisiert ist, sondern abhängig von unseren Skalen und der Anzahl an Beobachtungen. Daher können wir nicht mehrere Zusammenhänge anhand des Chi-Quadrat-Koeffizienten vergleichen.

Beachte
Anders als bei der Kovarianz ist beim Chi-Quadrat auch die Richtung des Zusammenhangs nicht erkennbar, da wir nun mit nominalen Daten arbeiten.
Wusstest du schon, dass ...

Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?

Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.

Erfahre mehr zur Korrektur

Chi-Quadrat in 4 Schritten bestimmen

In der Tabelle sind die einzelnen Berechnungsschritte am Beispiel erklärt.

Allgemein Beispiel
1 Berechne zunächst die erwarteten absoluten Häufigkeiten.

Beachte
Bei dem erwarteten Wert gehen wir davon aus, dass die Merkmale unabhängig voneinander sind. Dies bedeutet, dass es keinen Zusammenhang zwischen den Ausprägungen der beiden Merkmale gibt.

Verwende zur Bestimmung der erwarteten Werte (ñij) folgende Formel:
\tilde{n}_{ij}={\frac{{{n}_{i}.}*{{n.}_{j}}}_{n}}
Dabei ist ni. die Gesamtanzahl i-ter Spalte und n.j die Gesamtanzahl von Zeile j.

 Wir fügen die einzelnen Werte in die Formel \tilde{n}_{ij}={\frac{{{n}_{i}.}*{{n.}_{j}}}_{n}} ein.

    \begin{align*} \tilde{n}_{11}={\frac{{130}*{70}}_{250}}=36 \end{align*}

    \begin{align*} \tilde{n}_{11}={\frac{{120}*{70}}_{250}}=34 \end{align*}

    \begin{align*} \tilde{n}_{11}={\frac{{130}*{80}}_{250}}=42 \end{align*}

    \begin{align*} \tilde{n}_{11}={\frac{{120}*{80}}_{250}}=38 \end{align*}

    \begin{align*} \tilde{n}_{11}={\frac{{130}*{100}}_{250}}=52 \end{align*}

    \begin{align*} \tilde{n}_{11}={\frac{{120}*{100}}_{250}}=48 \end{align*}

 

Die Tabelle gibt dir einen Überblick über die beobachteten und die erwarteten Werte der einzelnen Merkmalskombinationen.

Jura NW SW ∑
beob. erw. beob. erw. beob. erw.
W 38 36 35 42 57 52 130
M 32 34 45 38 43 48 120
∑ 70 80 100 250

 
2 Subtrahiere nun den erwarteten Wert vom beobachteten Wert und quadriere anschließend das Ergebnis:

    \begin{align*} {(n_{ij} - {\tilde{n}_{ij})^2}} \end{align*}

 Wir ziehen den beobachteten Wert vom erwarteten Wert ab und nehmen das Ergebnis hoch 2.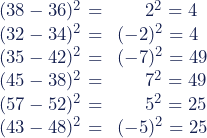
\\ (38 - 36)^2 = \,\,\,\,\,\,\,\,\,\,\,\, 2^2 = 4 \\ (32 - 34)^2 = \,\,\,(-2)^2 = 4 \\ (35 - 42)^2 = \,\,\,(-7)^2 = 49 \\ (45 - 38)^2 = \,\,\,\,\,\,\,\,\,\,\,\, 7^2 = 49 \\ (57 - 52)^2 = \,\,\,\,\,\,\,\,\,\,\,\, 5^2 = 25 \\ (43 - 48)^2 = \,\,\, (-5)^2 = 25
3 Dividiere die Ergebnisse aus Schritt 2 durch den erwarteten Wert:

    \begin{align*} {\frac {(n_{ij} - \tilde{n}_{ij})^2}{\tilde{n}_{ij}}} \end{align*}

 Wir teilen die Ergebnisse aus Schritt 2 durch die erwarteten Werte aus der Tabelle.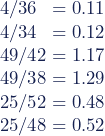
\\ 4 / 36 \,\,\,= 0.11 \\ 4 / 34 \,\,\,= 0.12 \\ 49 / 42 = 1.17 \\ 49 / 38 = 1.29 \\ 25 / 52 = 0.48 \\ 25 / 48 = 0.52
4 Zuletzt bilde die Summe aus den Ergebnissen aus Schritt 3.

Das Ergebnis ist der Chi-Quadrat (χ2) Wert.

 Wir addieren alle Ergebnisse aus Schritt 3:

0.11 + 0.12 + 1.17 + 1.29 + 0.48 + 0.52 = 3.69

In unserem Beispiel haben wir ein Chi-Quadrat (χ2) von 3.69.

Formel zum Chi-Quadrat

Die Formel stellt die oben erläuterten Schritte zur Berechnung des Chi-Quadrats zusammengefasst dar.

    \begin{align*} X^2 = {\sum}^m _{i=1}{\sum}^k _{j=1} {\frac {{(n_{ij} - \tilde{n}_{ij})^2}}{\tilde{n}_{ij}}} \end{align*}
X^2 Chi-Quadrat
m Gesamtanzahl der Zeilen
k Gesamtanzahl der Spalten
n_{ij} absolute Häufigkeit der Merkmalskombination in i-Zeile und j-Spalte (beobachteter Wert)
\tilde{n}_{ij} erwarteter Wert der absoluten Häufigkeit der Merkmalskombination in i-Zeile und j-Spalte
Merke
Wir können die Formel auch vereinfacht in Worten schreiben als:

    \begin{align*} X^2 = \sum {\frac {({beobachteter} - {erwarteter \,Wert})^2}{erwarteter \,Wert}} \end{align*}

Vom Chi-Quadrat zum Kontingenzkoeffizienten

Der Chi-Quadrat-Koeffizient ist ein nicht standardisiertes Zusammenhangsmaß und daher nur begrenzt vergleichbar.

Um konkrete Schlüsse und Vergleiche zu ziehen, können wir den Chi-Quadrat Wert in den Kontingenzkoeffizienten nach Pearson oder auch Cramers V umwandeln.

Wusstest du schon, dass ...

Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?

Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.

Erfahre mehr zur Korrektur

Kreuztabelle

Die Kreuz- oder auch Kontingenztabelle stellt die Zusammenhänge nominaler Daten dar.

In einer vollständigen Kreuztabelle können wir die relativen und absoluten Häufigkeiten der einzelnen Merkmalsausprägungen ablesen.

Jura NW SW Summe (Zeile)
Weiblich 38 0.29 35 0.27 57 0.44 130
0.54 0.25 0.44 0.23 0.57 0.38
Männlich 32 0.27 45 0.38 43 0.36 120
0.46 0.21 0.56 0.30 0.43 0.29
Summe (Spalte) 70 80 100 150

Die Zellen der Kreuztabelle können wir dabei wie folgt lesen:

Allgemein: Im Beispiel (weibliche Jura-Studentin):
Zellhäufigkeit
(absolut)		 Anteil an Zeilen-
gesamtsumme (%)
Anteil an Spalten-
gesamtsumme (%)		 Anteil an Gesamtanzahl (%)
38 38 / 130
= 0.29
38 / 70
= 0.54		 38 / 150
= 0.25

In dem Beispiel können wir ablesen, dass …

… 54 % aller Jura-Studierenden weiblich sind (0.54 in der Tabelle).
… 29 % aller weiblichen Teilnehmerinnen Jura studieren (0.29 in der Tabelle).
… 25 % aller Teilnehmenden weiblich sind und Jura studieren (0.25 in der Tabelle).

Merke
Die Summen der Zeilen und Spalten in der Kreuztabelle werden auch Randverteilungen genannt.

Häufig gestellte Fragen

Was sagt mir der Chi-Quadrat-Wert?

Chi-Quadrat (χ2) gibt dir Auskunft über den Zusammenhang von zwei nominal- oder ordinalskalierten Variablen.

Ist der Chi-Quadrat Wert standardisiert?

Nein, der Chi-Quadrat-Koeffizient ist nicht standardisiert und daher nur begrenzt vergleichbar. Wir können den Chi-Quadrat-Koeffizienten allerdings in den Kontingenzkoeffizienten nach Pearson oder Cramers V umrechnen.

Diese Koeffizienten sind standardisiert und daher gut vergleichbar.

Was ist eine Kreuztabelle?

In der Kreuztabelle sind die absoluten und relativen Häufigkeiten von Kombinationen bestimmter Merkmalsausprägungen dargestellt.

Diesen Scribbr-Artikel zitieren

Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.

Benning, V. (2023, 11. April). Chi-Quadrat verstehen und berechnen - mit Beispiel. Scribbr. Abgerufen am 11. November 2024, von https://www.scribbr.de/statistik/chi-quadrat/

Diesen Artikel zitieren
War dieser Artikel hilfreich?
Valerie Benning

Hi, ich bin Valerie und schreibe zur Zeit selbst meine Masterarbeit in Psychologie. Meine Erfahrungen aus dem Studium teile ich gerne, damit Studierenden statistische Themen leichter fallen.

Das hat anderen Studierenden noch gefallen

Kovarianz verstehen und berechnen

Die Kovarianz gibt dir Auskunft über den Zusammenhang von zwei metrischen Variablen. Wie du sie berechnest, erklären wir im Artikel.
132

Die Lageparameter erklärt mit Beispielen

Lageparameter ist der Überbegriff für Werte, die wir als arithmetisches Mittel, Median und Modus bestimmen. Wir erklären sie dir hier.
36

Den Kontingenzkoeffizienten verstehen, bestimmen und interpretieren

Der Kontingenzkoeffizient nach Pearson gibt uns Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren Variablen.
42